In continuation with the previous article on IBPS PO Prelims 2018 – Memory Based DI questions with unique solutions part 1, we will be taking forward these series of questions of Data Interpretation to the next part with some interesting concepts. Meanwhile if you haven’t read that article, you can do so by following this link – click here
Institute of Banking Personnel Selection (IBPS) has conducted the Prelims Exam for the post of Probationary Officers successfully across the country in the month of October 2018. The exam was conducted in four different slots. These DI questions were asked in one of the four slots of IBPS PO prelims exam.
DI – Set 2
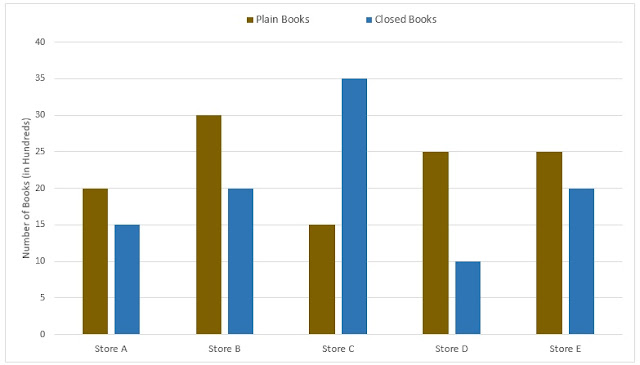
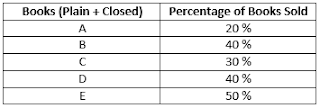
Study the data carefully in Bar Diagram, illustrating the number of Plain books and Closed books kept and sold in different stores. Answer the questions given below.
Q.1) Find the difference between the total number of books (Plain + Closed) sold by Store A and that by Store B.
Solution :
Total books in Store A = 2000 + 1500 = 3500
Sold books by Store A = 20% of 3500 = 1/5 × 3500 = 700
Total books in Store B = 3000 + 2000 = 5000
Sold books by Store B = 40% of 5000 = 2/5 × 5000 = 2000
Required Difference = 2000 – 700 = 1300 [ANS]
Q.2) Find the ratio of Plain books sold by Store A and plain books sold by Store E.
Solution :
Total books sold by Store A = 20% of 3500 = 1/5×3500 = 700
Now we have to find the number of plain books sold by Store A, to do so we need to distribute them in given ratio of Plain books and Closed books in Store A
Plain books : Closed books = 2000 : 1500 = 4 : 3
So,
The number of Sold plain books by A = 4/7×700 = 400
Similarly, Total books sold by Store E = 50% of (2500+2000) =1/2 × 4500 = 2250
Now given Ratio of Plain books : Closed books in E = 2500 : 2000 = 5 : 4
So,
The number of Sold plain books by E = 5/9 × 2250 = 1250
Finally Required Ratio = 400 : 1250 = 8 : 25 [ANS]
Q.3) What percentage of closed books of Store B is of closed books of Store C ?
Solution :
Closed books in B = 2000
Closed books in C = 3500
Required Percentage = (2000/3500) × 100 = 4/7 × 100
Now don’t solve this by traditional division method. We all know that the percentage vato fractional value of 1/7 (i.e. 1/7 × 100) is equal to 14.28.
Hence,
4/7 = 4 × (1/7) = 4 × 14.28 = 57.14% [ANS]
Q.4) Find the number of unsold books (plain + closed) left in Store D ?
Solution :
Total number of books in Store D = 2500 + 1000 = 3500
Now,
since sold books in D = 40%
then unsold books in D = 100% – 40% = 60%
Hence required number of unsold books = 60% of 3500
Here to calculate (60% of 3500) we have two methods.
Method I :
60% of 3500 = (50% + 10%) of 3500 = 50% of 3500 + 10% of 3500
= 1/2 × 3500 + 1/10 × 3500 = 1750 + 350 = 2100 [ANS]
Method II : There is a property of Percentage that,
x% of y = y% of x
Here we will apply the same rule,
Split the number 3500 into two parts = 3000 + 500
So,
60% of (3500) = 60% of (3000 + 500) = 60% of 3000 + 60% of 500
or 3000% of 60 + 500% of 60,
And we all know 100% of 60 = 60
So,
3000% of 60 = 30 × (100% of 60) = 30 × 60 = 1800
Also, 500% of 60 = 5 × (100% of 60) = 5 × 60 = 300
Required Total = 1800 + 300 = 2100 [ANS]
(Use whichever method, you find it easier and less time consuming)
Q.5) What is the Average number of Plain Books in Store B, Store C and Store D ..?
Solution :
No. of plain books in B = 3000
No. of plain books in C = 1500
No. of plain books in D = 2500
Average = (3000 + 1500 + 2500)/3
Wait now !! Instead of using the traditional method of adding the numbers and dividing by 3, we will use some smart techniques. As we all know that Average is the equal distribution among ‘n’ number of elements.
So, by the same concept.
Let us assume, Average = 2000
Thus inorder to make all of them equal to 2000, we will be balancing and compensating the values with each other.
B = 2000 (Extra = 3000 – 2000 = 1000)
C = 2000 (Extra = 1500 – 2000 = -500)
D = 2000 (Extra = 2500 – 2000 = 500)
Now distribute Extra part equally among the three.
Average = 2000 + (Extra / 3)
= 2000 + {(1000 + (-500) + 500) / 3}
= 2000 + (1000/3)
= 2000 + 333.33 = 2333.33 [ANS]
Note : Try to do all the calculations mentally, as described above and cut short the sentences written above, they are just to make you understand. Although Explanations may look difficult or tedious, but once understood it will be easy and less time consuming to deal with.
That’s all in this article, if there is any feedback or suggestions, then feel free to comment below. And don’t forget to share this with your near and dear ones. Sharing is Caring..!
Thank You !!